resilikon.blogg.se - Vector 2d collision

Vector 2d collision how to#
Vector 2d collision update#
Vector 2d collision free#

So your target position could then be your character current position in start of avoid + avoidDir multiplied with some distance.

Bounding volume collision detection with THREE.jsĬrafty. var avoidDir Vector2.Perpendicular( transform.up) Since you are using 2D collisions, youll be moving in XY-plane.

Building up a basic demo with Pla圜anvas.

Building up a basic demo with Babylon.js.

Using WebRTC peer-to-peer data channels.

This site is a place for me to write about whatever I happen to be working on. If the collision involves a vertical or horizontal line, the axis will be 'x' or 'y'.

Vector 2d collision free#

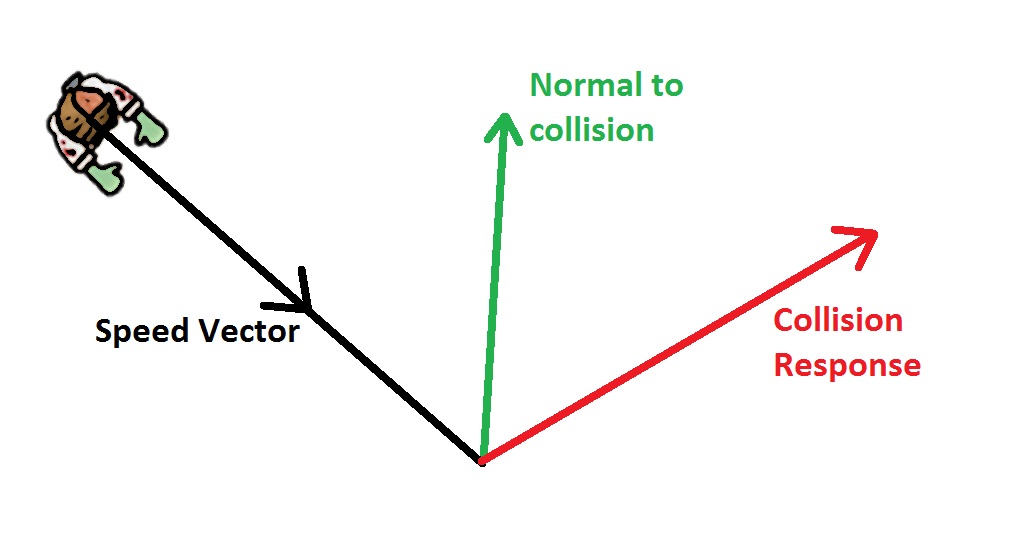
I'm a former computer science student at UCLA, and a game developer in my free time. Basically a vector from one entity to the other. These problems and others have to be solved by more robust physics engines, but I hope this was a useful introduction to physics of rigid bodies in 2D. Others require a more complex approach of considering more than two objects at a time. Some problems with objects clipping through one another can be solved by not applying the impulse force unless j > 0. More importantly there can still be objects clipping through one another, because when a lighter object is sandwiched between two heavy objects it doesn't transfer force from one heavy object to another, and is often squeezed through one of the heavier objects. collisions only - no gravity, rigid body handling, or complex solvers. consistent vector/matrix/line representation. None satisifed all of these criteria: consistent API interface. It also handles objects touching each other at rest rather poorly. There are many javascript collision routines and libraries for 2d. For one, it doesn't apply any friction forces, which you generally do want for more realism. Express momentum as a two-dimensional vector Write equations for momentum conservation in component form Calculate momentum in two dimensions, as a vector. This method works well for two rigid bodies colliding by themselves, but it has some limitations. There is a heavy rectangular object that is not drawn but bounds the other objects so that they stay interacting longer instead of flying off the screen. You can use the slider to change the coefficient of restitution from 0 to 1. It creates some arbitrary polygons with randomized velocities, sizes, etc and lets them interact for a bit before replacing them with a new set of objects. This demo brings together both collision detection and response. Press the mouse button ( Do not release it) to see the velocity vectors just after the collision. $$m_1 v = m_1 u_1 + m_2 u_2$$ $$\frac)$$ Demo java-2D-CollisionDetection / CollisionDetection. When the two objects collide, the animation will be suspend. We have two unknowns ( u 1, u 2) so we can just combine the conservation equations for momentum and kinetic energy to solve for u 1 and u 2. The velocities of m 1, m 2 after collision will be u 1, u 2 respectively. Click near the tip of the velocity vector and drag the mouse button. Click left mouse button to suspend the animation. Two circular objects will move with pre-defined velocity (yellow arrow). Remember that converting a convex shape in 2D to an array of 2D planes was useful for collision detection You could detect if a point was inside any convex. We have a mass m 1 moving at a velocity v colliding with another mass m 2. Lets consider collisions in two dimension: Press Start to begin the animation. 1D Collision Responseįirst I'm going to briefly go over 1D elastic collision response. Let x1, x2, y1, and y2 be the x and y coordinates of the centers of the circles. This is done by taking a vector whose components are the difference between the coordinates of the centers of the circles.

Vector 2d collision how to#

I found this after getting stuck figuring out how to calculate the magnitude of the impulse exchanged, so thanks to the authors for making that available. tangent to the circles' surfaces at the point of collision. There is a great paper here which describes the same collision detection/response algorithm in 3D, and I've used the same notation in case anyone reads both. To implement this form of reflection in code, we can use this function: vector2D axisAlignedCollision(. At the end I'll show how to tweak the formula slightly to change the elasticity with a coefficient of restitution. I'm going to go about this with perfectly elastic collision in mind, so both momentum and kinetic energy will be conserved.

Vector 2d collision update#

Today I'll be explaining how to update the linear and angular velocity of these polygons in response to that collision. This is a followup to my previous article regarding collision detection between arbitrary polygons.